What is Section Modulus (Z)?

Section modulus is a geometric property of a flexural member like a beam that defines the strength of a given section. It is defined as the ratio of the moment of inertia of a section (I) about the neutral axis to the distance of the outermost layer from the neutral axis.

Z = I/y_max

Here, I is the Moment of Inertia (M.O.I) about the neutral axis and y_max is the distance of the outermost layer from the neutral axis.

As section modulus represents the strength of a given section, the higher the value of section modulus, the higher its strength.

Section modulus can be of two types: elastic section modulus (Z_e) and plastic section modulus (Z_p).

In this article, we will discuss the detailed concept of section modulus and the formula to find the elastic and plastic section modulus of a section.

Bending Stress (σb) and Section Modulus (Z)

As per the simple bending theory, a section resists the bending moment by having bending stresses. If we consider a section as shown in figure 2, with neutral axis NA, subjected to bending will undergo compressive stresses at the top and tension stress at the bottom.

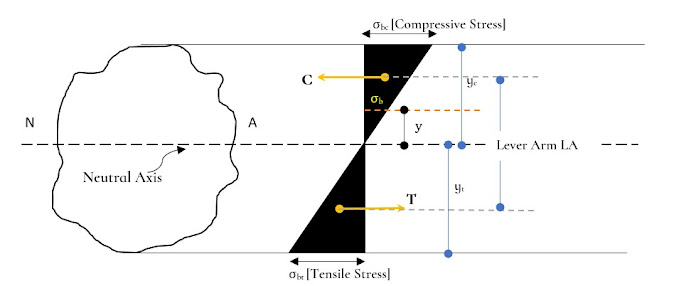
Fig.2. Stress Distribution Along the Cross-Section Subjected to Load

We know the bending equation is

M/I = σ/y = E/R

Where,

• M = Bending moment at the section, I= Moment of inertia of the section
• E = Modulus of elasticity of the beam
• σ = Bending stress or flexural stress at a distance y from the neutral axis
• R= Radius of Gyration

In the figure below bending stress at a distance ‘y’ is σ_b , while the compressive stress at extreme fibre is σ_bc at a distance of ‘y_c’ and the tensile stress at extreme fibre is σ_bt at a distance of ‘y_t’.

From the bending equation,

At the extreme top fibre, the compressive stress is given by:

σ_bc = M/I . y_c = M/Z_c

Here, Z_c is the section modulus of the section at compression;

Similarly, the tensile stress at the extreme bottom fibre is given by:

σ_bt = M/Z_t;

Where Z_t is the section modulus of the section at tension.

Section Modulus (Z) for a Symmetrical Section

When the section is symmetrical, i.e. the area distributed around the neutral axis is the same and symmetrical about the neutral axis, the stress distribution will be symmetrical about NA. This means:

y_c = y_t = y_max ;

σ_bc = σ_bt = M/I . y_max = M/Z

σ_bc = M/Z

Z is the section modulus of the given symmetrical section. From the derivation, it is clear that the section modulus is dependent on the disposition of the area of the section with respect to the centroidal axis.

Determination of Section Modulus

We know that a rectangular beam that is subjected to a gradually increasing load is subjected to bending. As the load increases, the bending stress increases. The bending stress can be given by the equation:

σ_b = M. (y/I) = M/Z;

Fig.3. Plastic Bending of Beams

This bending history of the beam can be summarized to go through three stages, namely:

1. Elastic stage bending
2. Elastoplastic stage bending
3. Fully plastic stage bending

Let’s discuss the elastic stage bending and plastic stage bending in detail.

1. Elastic stage bending

At this stage of bending, the stress σ increases with the increase in load. At this state, σ < σy (yield stress). The stress is directly proportional to strain (e) as per Hooke’s law until the limit of proportionality. (Figure 3 (b-2))

At σ = σy, The first yielding of the extreme fibres of the section develops. This results in a bending moment called Yield Moment My.

My = σ_y. Z

2. Elasto Plastic Stage Bending

At this stage, the section is partially yielded or plasticised. After reaching yield, extreme fibres spread inwards. This results in a state where the neutral axis no longer passes through the centroid. The middle portion of the beam at a depth of 2y_o remains elastic and is called as the elastic core.

Fig.4. Beam Cross-Section at Partially Plastic Stage

Hence, the total moment of resistance is contributed from the moment (M1) from the elastic core section and the plastic core section i.e. M2.

After derivation,

M = 1.4965 My

Hence, it is clear that at this stage, the total moment of resistance M is greater than the yield moment My.

Note: The detailed derivation is explained in “Design of Steel Structures, B.C. Punmia, Page No: 807”

3. Plastic Stage Bending

At the plastic stage, the stress in both tensile and compressive zone is equal to the yield stress and now have to pick up higher stresses. This process continues till the plastic zone gradually and progressively advances towards the neutral axis from either side. 

Here the NA shifts to a new location called as the equal area axis (Figure 3 (a))whose location is determined by the fact that the total compressive force is equal to the total tensile force over the cross-section. ( Equal area axis does not pass through the centroid at this stage).

Fig.5. Beam Cross-Section at Fully-Plastic Stage

As shown in the figure above, the two plastic zones now finally meet, as the entire cross-section of the beam reaches the yield stress and becomes fully plastic.

When the beam cross-section reaches the fully plastic stage, the beam rotates substantially at the section, i.e. it becomes incapable of resisting any further increase in the loads and in effect behaves like a rusty hinge with a constant moment of resistance.

The bending moment that causes the entire cross-section to remain plastic is called the Plastic Moment called Mp, which is given by:

Mp = σ_by. Zp

Here, Zp is the section modulus in a plastic stage called as the Plastic Section Modulus.

As mentioned above, Zp is used for material where plastic behaviour or irreversible behaviour is dominant. The plastic section modulus merely depends on the location of the plastic neutral axis (PNA). 

PNA is defined as the axis that splits the cross-section such that the compression force from the area in compression equals the tension forces in tension.

If the areas above and below PNA are A₁ and A₂, the total moment of resistance at plastic stage Mp = Moment due to area A₁ and Moment due to area A₂

Mp = A₁σ_y. y₁ + A₂.σ_y.y₂

M_p = σ_y . (A₁ y₁ + A₂.y₂)

 Zp = A₁ y₁ + A₂.y₂

When the area A1=A2=A

Zp = A/2 [y1 +y2]

Hence, Zp is the first moment of area about the neutral axis.

If the cross-section has constant yielding stress, the area above and below PNA is equal. But if it is a composite section, it may differ.

Elastic Section Modulus (Ze) and Plastic Section Modulus ( Zp) – Shape Factor

Elastic Section Modulus (Ze)

Elastic section modulus (Ze) is defined for cross-sections that are under load conditions up to the yield point i.e. during the elastic stage bending. This occurs at yield moment My. Hence

My = σ_y . Ze

Ze = I/y_max

_{Where I is the second moment of inertia of the cross-section.}

Plastic Section Modulus (Zp)

While plastic section modulus (Zp) is defined for cross-section where plastic behaviour is dominant. It occurs at the plastic moment Mp;

Mp = σ_y. Zp

Zp = A/2 [y1 +y2]

Shape Factor (S)

Shape factor (S) is the ratio of the plastic moment to yield moment.

S = Mp/My = (σ_y . Ze)/ σ_y.Zp = Zp/Ze

 ALSO READ MORE ON: STRUCTURAL ANALYSIS