Area Computation in Surveying | Simpson's One-Third Rule

Simpson's one-third rule is one method of area computation method that comes under "Area computation by taking offsets from baseline" in civil engineering surveying calculations. Other methods coming under this category are the mid-ordinate rule, trapezoidal rule, and average ordinate rule. All these methods are employed when the boundary line is nearly straight.

When the boundary line is curved or slightly deviates from a straight line, we employ Simpson's one-third rule. Here, the curved portion of the boundary line is assumed to be a parabolic curve. To proceed with the calculations, we draw offsets from the baseline enclosing the curved portion of the boundary line.

No Time to Read: Watch Video Here>> 

Simpson's One-Third Rule

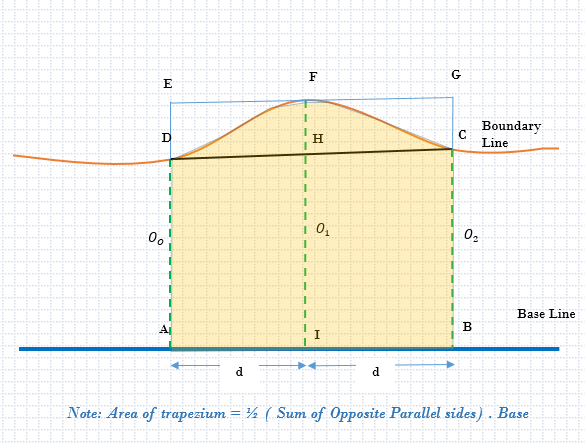
Consider a curved boundary line, whose curved parabolic portion DFC is under consideration. We consider a baseline AB, from which offsets need to be taken perpendicular and parallel to each other. They form O_o, O_1, and O₂. (Fig.1).

Simpson's One-Third Rule

The corresponding chord of the parabolic curve DFC is DC. This will finally give a trapezoid and a segment. The total area of the shaded portion, ABCFD needed to be determined as shown in fig.2.

Area = Area of the trapezium + Area of Segment

Consider 'n' as the number of ordinates.

Simpson’s one-third rule states that the total area is equal to the sum of the two end ordinates plus four-time the sum of the even intermediate ordinates plus two times the sum of the odd intermediate ordinates, the whole divided by the one-third of the common interval between them.

Simpson’s rule as explained can be applied only when the number of divisions of the area is even i.e. the total number of ordinates is odd. If there is an odd number of divisions, (resulting in an even number of ordinates), the area of the last division must be calculated separately and added to the above equation.

Also Read: Surveying