Search This Blog
Most Popular
Categories
- Building Construction (86)
- Building Materials (83)
- Columns (2)
- Concrete Beam (3)
- Concrete Construction Techniques (4)
- Concrete Mix Design (13)
- Concrete Repair (14)
- Concrete Slab (10)
- Construction Equipment (16)
- Construction News (7)
- Design of Structures (15)
- Engineering Drawing (1)
- Estimation (3)
- Geotechnical engineering (26)
- Highway Engineering (11)
- Innovations (32)
- Material Testing (10)
- Matrix Analysis of Structures (2)
- Mechanical Engineering (3)
- Strength of Materials (2)
- Structural Analysis (13)
- Structural Design (22)
- Structures (17)
- Transportation Engineering (9)
Area Computation in Surveying | Simpson's One-Third Rule
Simpson's one-third rule is one method of area computation method that comes under "Area computation by taking offsets from baseline" in civil engineering surveying calculations. Other methods coming under this category are the mid-ordinate rule, trapezoidal rule, and average ordinate rule. All these methods are employed when the boundary line is nearly straight.
When the boundary line is curved or slightly deviates from a straight line, we employ Simpson's one-third rule. Here, the curved portion of the boundary line is assumed to be a parabolic curve. To proceed with the calculations, we draw offsets from the baseline enclosing the curved portion of the boundary line.
No Time to Read: Watch Video Here>>
Simpson's One-Third Rule
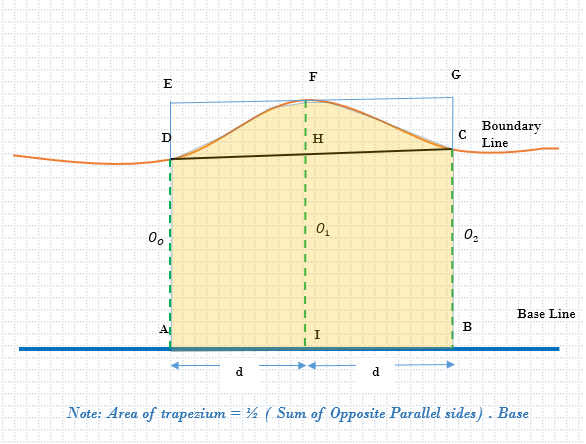
Consider a curved boundary line, whose curved parabolic portion DFC is under consideration. We consider a baseline AB, from which offsets need to be taken perpendicular and parallel to each other. They form Oo, O1, and O2. (Fig.1).
 |
| Simpson's One-Third Rule |
Simpson’s one-third rule states that the total area is equal to the sum of the two end ordinates plus four-time the sum of the even intermediate ordinates plus two times the sum of the odd intermediate ordinates, the whole divided by the one-third of the common interval between them.
Simpson’s rule as explained can be applied only when the number of divisions of the area is even i.e. the total number of ordinates is odd. If there is an odd number of divisions, (resulting in an even number of ordinates), the area of the last division must be calculated separately and added to the above equation.
Also Read: Surveying




0 Comments
Commenting Spam Links Are Against Policies