Search This Blog
Most Popular
Categories
- Building Construction (87)
- Building Materials (86)
- Columns (2)
- Concrete Beam (3)
- Concrete Construction Techniques (6)
- Concrete Mix Design (15)
- Concrete Repair (14)
- Concrete Slab (11)
- Construction Equipment (17)
- Construction News (7)
- Design of Structures (20)
- Engineering Drawing (1)
- Estimation (3)
- Geotechnical engineering (26)
- Highway Engineering (11)
- Innovations (34)
- Material Testing (11)
- Matrix Analysis of Structures (2)
- Mechanical Engineering (3)
- Strength of Materials (2)
- Structural Analysis (13)
- Structural Design (24)
- Structures (17)
- Transportation Engineering (9)
Bearing Capacity of Foundations – Terzaghi’s Formula for Square, Circular & Rectangular Footings
Team Prodyogi
March 10, 2022
Learn how Terzaghi’s 1943 bearing capacity equation defines the strength of soils under square, rectangular, and circular footings. Understand the role of cohesion, friction angle, and shape factors, and see how to apply general and local shear failure equations for both cohesive and cohesionless soils. Perfect for civil engineering students and professionals.
The above equations were derived from the assumptions of general shear failure. When local shear failure comes into play, the shear parameters in the equations i.e. the c and ф are reduced to a lower limit. Hen e, here instead of c we use Ĉ = 0.67c; and instead of Ф, we use ቔ = 0.67tanФ;
Terzaghi (1943) developed a rational bearing capacity equation for strip footing, by assuming the bearing capacity failure of the foundation in general shear mode. Terzaghi's bearing equation is given by:
qu = CNc + γ1DfNq + 0.5Bγ2Nγ
- qu= Ultimate Bearing Capacity of the soil
- C= Cohesion
- γ1,γ2= Unit weight of the soil above and below the footing level
- Nc,Nq,Nγ= Bearing capacity factors that are a function of friction angle
- Df= Depth of the foundation below the ground level
- B = Width or diameter of the footing
- L= length of the footing
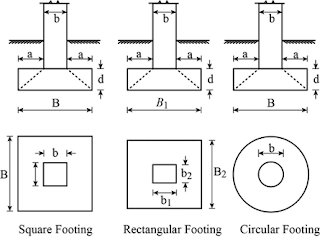 |
| Square, Rectangular, and Circular Strip Footings |
Bearing Capacity Equation for Square, Rectangular, and Circular Foundations - General Shear Failure
Terzaghi modified the above bearing capacity equation by introducing shape factors for different shapes of the foundation. Then for
1. Square Foundations
qu = 1.3CNc + γDfNq + 0.4BγNγ
2. Circular Foundations
qu = 1.3CNc + γDfNq + 0.3BγNγ
3. Rectangular Foundations
Bearing Capacity Equation for Square, Rectangular, and Circular Foundations - Local Shear Failure
The values of Nc, Nq, and Nγ, also change to reduced values that are obtained from Terzaghi's bearing capacity factors for the general shear failure graph, where the bearing capacity factors corresponding to reduced Ф i.e, 0.67tanФ, must be determined.
Then the bearing capacity for:
1. Strip Foundation
2. Square Foundation
3. Circular Foundation
4. Rectangular Foundation
When the soil is cohesionless, the cohesion factor c = 0; If c =0; the bearing capacity factor Nc = 0; Then the equations for qu can be modified accordingly.
If the soil is cohesive, then the angle of frictional resistance, Ф = 0; then the bearing capacity factors from the graph above, Nγ = 0; Nq= 1; and Nc = 5.7; Based on which the qu equation is determined.
Most Visited
Soil Sampling Methods| Undisturbed and Disturbed Samples
November 08, 2023
Boring Methods for Soil Exploration
November 02, 2023
Steel Column Connected to Concrete Masonry Wall
October 11, 2017
How to Choose Good Quality Aggregates for Construction?
August 10, 2021
Terzaghi's Equation: Soil Bearing Capacity for Foundations
March 02, 2022
What are Infiltration Wells?
April 15, 2024
Structure of Timber |Macrostructure and Microstructure
March 22, 2024
Search This Blog
MUST READ
What is PERT? Objectives, Pros & Cons
September 10, 2017
Terzaghi's Equation: Soil Bearing Capacity for Foundations
March 02, 2022
Contact Form
Footer Menu Widget
Created By SoraTemplates | Distributed By Gooyaabi Templates






0 Comments
Commenting Spam Links Are Against Policies