What is a Column in Construction?

A column or pillar in civil engineering and architecture is an isolated vertical member that transmits the loads from the above structural element to the below member through compression. They are generally categorized as vertical members, whose length is three times greater than the least cross-sectional dimension of the column.

These structural members are relatively slender that are designed primarily to support axial compressive loads applied to the ends of the members. 

Columns for building construction can be made out of steel, reinforced concrete, wood, or composite materials.  It can take square, round, I, etc cross-sections based on the load to be sustained and the material used for column construction.

This article outlines the basic characteristic behavior and features of columns in building structures along with their behavior under the action of loads.

Structural Behaviour of Columns

The general arrangement of building elements in a structure and their load-path diagram is shown in the below figure. It is mainly comprised of footing, columns, beams, and slabs. Columns are the vertical members that span between the substructure to the superstructure.

The columns take the axial compressive loads coming from the top beam and slab elements and transfer them safely to the footing and then to the soil. It has an important role in the load transfer mechanism of a complete building structure. A building structure does not exist without column members.

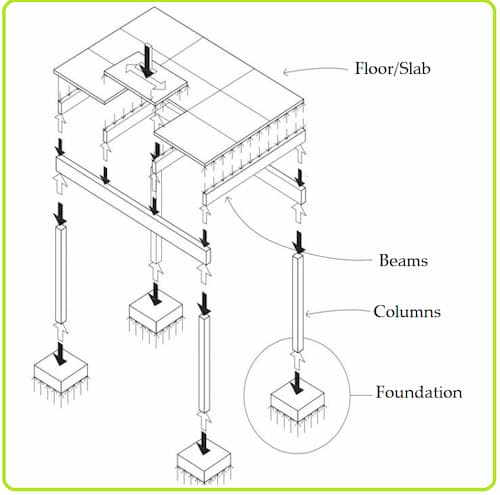Load-Path Diagram of a Building Structure

Every column is designed for a design compressive strength to sustain the most expected axial load over it. Failure occurs when the direct stress from the axial load exceeds the compressive strength of the material that is available in the column section. 

Consider a column section as shown below. The external forces create internal stresses within the structural elements that contribute to sustaining the external force. 

As shown in the figure, the kern area is the central area of any horizontal section of a column within which the resultant of all the compressive loads must pass to expect only compressive stresses. If compressive loads are applied beyond this section, it results in tensile stresses developing in the section. 

Behavior of Columns Under Axial Load

Columns can fail mainly due to crushing or buckling phenomena. Consider a perfectly straight vertical column subjected to an axial load. With the increase in the axial load, the column goes through three conditions:

1. Stable equilibrium
2. Neutral equilibrium
3. Instability

The stable equilibrium condition exists when the vertical column is subjected to a lateral force between the two ends of the column which in turn results in a small lateral deflection that vanishes when the lateral force is removed.

Next, the lateral load is increased again till a condition is reached when the removal of the lateral load won’t result in recovery to the initial condition. This is the condition where the column is bent slightly when the load is removed. This condition of the column is in neutral equilibrium. The load at which the column reaches neutral equilibrium can be called a critical or buckling load.

Next, the state of instability is reached when the load beyond critical load would cause uncontrollable lateral deflections that are permanent and would result in complete collapse.

The failure of the column would result in sudden failure, unlike beams and slabs. Hence, it demands accurate design and careful construction.

Effective Length, Slenderness Ratio, & Radius Gyration of Columns

Effective Length of Column

The effective length of a column is the distance between the inflection points on a column that is subjected to buckling. When this portion of the column buckles, the entire column is subjected to failure. 

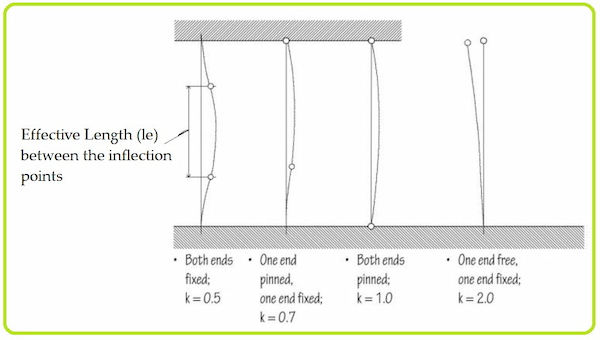Effective Length of Columns

Columns can be designed to have different end conditions as shown in the figure below. They can be:

1. Both ends fixed
2. One end pinned and one end fixed
3. Both ends pinned and 
4. One end free and other end fixed. 

So, while designing columns, the effective length of the column is calculated instead of the actual length. Effective length (le) is calculated using the effective length factor(k) and the actual length of the column(l). Hence, 

Effective Length of Column (le) = k.l

The effective length factor (k) is a coefficient for modifying the actual length of the column according to the end conditions of the column to finally obtain the effective length, as shown in the figure above. For example, from the figure, the value of k for a column whose ends are fixed is 0.5. If the actual length of the column is l = 2 meters, then the effective length is le = 0.5 x 2 = 1m. 

Radius of Gyration (r)

The radius of gyration is the distance from an axis at which the mass of a body may be assumed to be concentrated. The radius of gyration of a column is the square root of the quotient of the moment of inertia and the area. 

There can be two values of the radius of gyration as the moment of inertia can be calculated with respect to X and Y axis. 

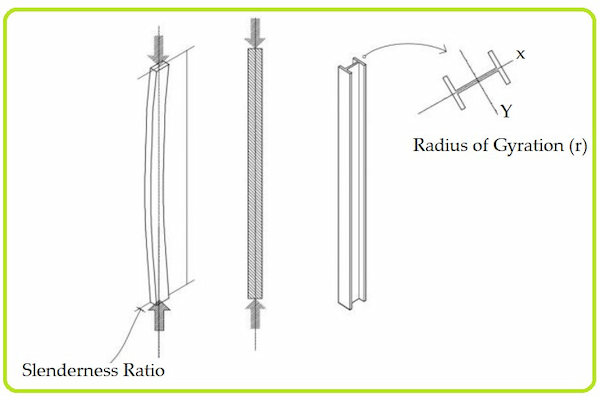Slenderness Ratio and Radius of Gyration of Columns

Slenderness Ratio of Column

The slenderness ratio of the column is defined as the ratio of its effective length (l) to its smallest radius of gyration (r). 

Slenderness Ratio = le/r

As mentioned above, while calculating the value of the slenderness ratio, the smallest value of r is taken. 

If the column section is symmetrical, the rxx and ryy will be the same. But, if it is unsymmetrical, the buckling tends to occur about the weaker axis or in the direction of the smallest dimension. 

The higher the slenderness ratio of the column, the lower the critical stress that will cause it to buckle. 

In the design of columns, the primary objective is to reduce the slenderness ratio by shortening the effective length or maximizing the radius of the gyration of its cross-section. 

Classification of Columns

Columns can be classified into several types based on:

1. Length-to-depth ratio
2. Loading condition
3. Cross-section

1. Column Types Based on L/d ratio

A column is said to be short if the ratio of the effective length of the column to its least lateral dimension is less than 12. If the l/d ratio is greater than 12, it's a long column.

Short columns fail by crushing, while long columns fail by buckling. Buckling can be defined as the sudden lateral or torsional instability of a slender structural member that is induced by the action of axial load before the yield stress limit of the material is reached. 

2. Column Type based on Loading Condition

Based on loading conditions, columns can be classified into:

• Axially loaded column
• Axially loaded and uni-axial bending
• Axially loaded and bi-axial bending

3. Column Type Based on Cross-Section

Types of Columns Based on Cross-Section

Based on the cross-section, the column can be classified into:

• Square column
• L-column
• T-Column
• Circular column
• Rectangular column

Also Read: How to Construct an R.C.C Column?

Sources:

1. European Building Construction IllustratedBy Francis D. K. Ching, Mark Mulville
2. Hameed Almamoori, Ali & Naser, Fatimah & H. Naser, Maryam. (2018). Studying The Effect Of Lateral Reinforcement On Circular Short Columns Behavior With/Without Steel Fibers  ‫. 16. 232.